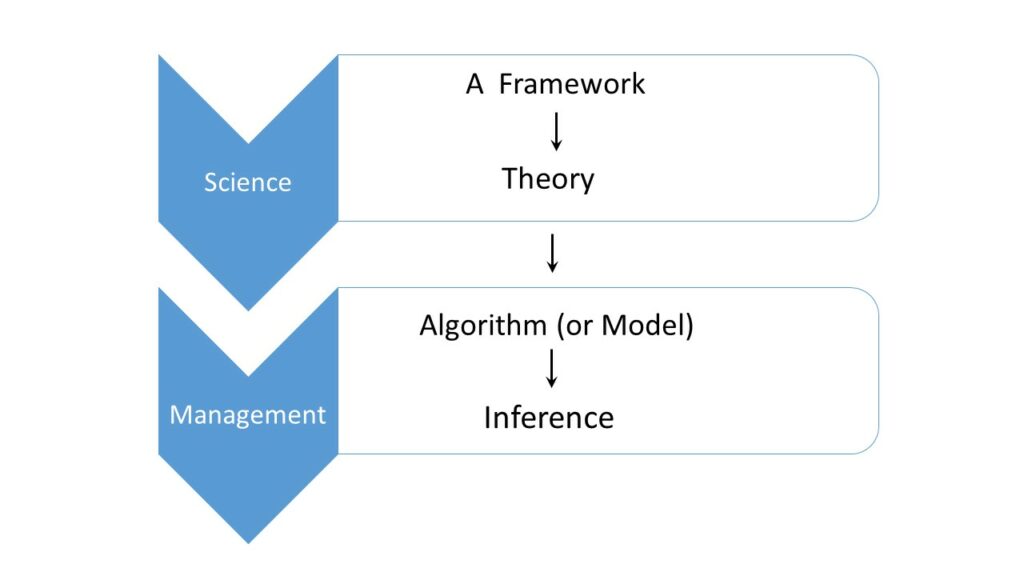
 Hierarchy and branches of Statistical Science
Hierarchy and branches of Statistical Science
 ]]>
]]>
by deepstatorg
 Hierarchy and branches of Statistical Science
Hierarchy and branches of Statistical Science
 ]]>
]]>
by deepstatorg
THEORY
Culture 1: Algorithm + Theory: the role of theory is to justify or confirm. Culture 2: Theory + Algorithm: From confirmatory to constructive theory, explaining the statistical origin of the algorithm(s)–an explanation of where they came from. Culture 2 views “Algorithms” as the derived product, not the fundamental starting point [this point of view separates statistical science from machine learning].PRACTICE
Culture 1: Science + Data: Job of a Statistician is to confirm scientific guesses. Thus, happily play in everyone’s backyard as a confirmatist. Culture 2: Data + Science: Exploratory nonparametric attitude. Plays in the front-yard as the key player in order to guide scientists to ask the “right question”.TEACHING
Culture 1: It proceeds in the following sequences: for (i in 1:B) { Teach Algorithm-i; Teach Inference-i; Teach Computation-i } By construction, it requires extensive bookkeeping and memorization of a long list of disconnected algorithms. Culture 2: The pedagogical efforts emphasize the underlying fundamental principles and statistical logic whose consequences are algorithms. This “short-cut” approach substantially accelerates the learning by making it less mechanical and intimidating. Should we continue to conform to the confirmatory culture or It’s time to reform? The choice is ours and the consequences are ours as well.]]>by deepstatorg
Richard Courant‘s view: “However, the difficulty that challenges the inventive skill of the applied mathematician is to find suitable coordinate functions.” He also noted that “If these functions are chosen without proper regard for the individuality of the problem the task of computation will become hopeless.” This leads me to the following conjecture: Efficient nonparametric data transformation or representation scheme is the basis for almost all successful learning algorithms–the Scientific Core of Data Analysis–that should be emphasized in research, teaching, and practice of 21st century Statistical Science to develop a systematic and unified theory of data analysis (Foundation of data science).]]>
by deepstatorg
Connectionist: Mathematicians who invent and connect novel algorithms based on new fundamental ideas that address real data modeling problems. Confirmatist: Mathematicians who prove why an existing algorithm works under certain sets of assumptions/conditions (post-mortem report). Albeit, the theoreticians of the first kind (few examples: Karl Pearson, Jerzy Neyman, Harold Hotelling, Charles Stein, Emanuel Parzen, Clive Granger) are much more rare than the second one. The current culture has failed to distinguish between these two types (which are very different in their style and motivation) and has put excessive importance on the second culture – this has created an imbalance and often gives a wrong impression of what “Theory” means. We need to discover new theoretical tools that not only prove why the already invented algorithms work (confirmatory check) but also provide the insights into how to invent and connect novel algorithms for effective data analysis – 21st-century statistics.]]>
by deepstatorg
Theoretical beauty x Practical utility = Impact of your work.